Projecting 3d Vector Onto A Plane

The vector x w is called the orthogonal projection of x onto w. These projections rely on visual perspective and aspect analysis to project a complex object for viewing capability on a simpler plane. That right there is v.

best vector stock art best software for designing company logo best pattern for vector plates best quality to copy farmers insurance logo vector best way to put company logo on milwaukee heat best sound company logo best place to get company stamp with logo best size to create vector logo

Rotated Region3 Rotated Boxes In 3d Space Scripting Helpers

Maths Plane Surface And Area Martin Baker

Distance From Point To Plane Math Insight

Projection Of 3d Features Onto A Plane Download Scientific Diagram

Projection Of The 3d Image Volume Onto A 2d Plane Download Scientific Diagram

Projection Of Point On Line In 3d Stack Overflow

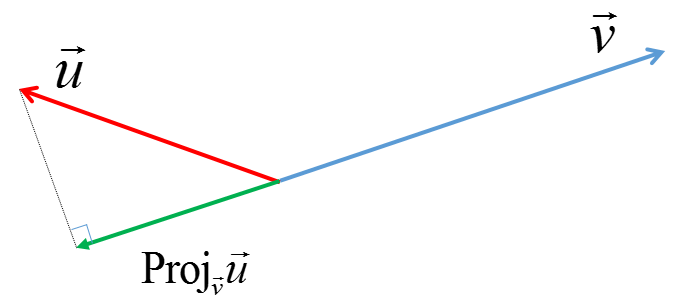
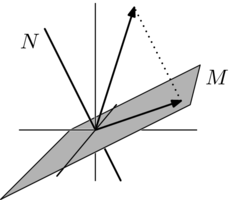
The projection of u onto a plane can be calculated by subtracting the component of u that is orthogonal to the plane from u.

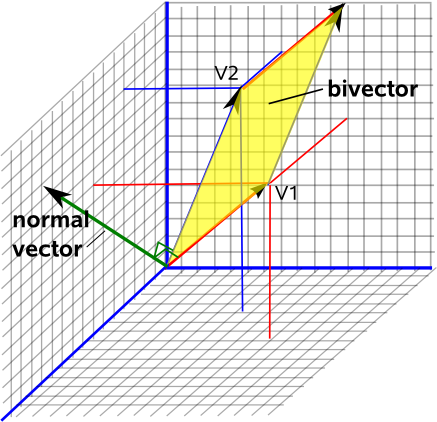
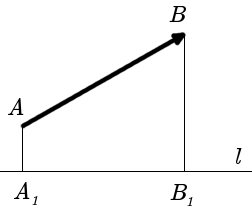
Projecting 3d vector onto a plane. And you could see that v is the projection onto the subspace capital v so this is a vector v is the projection onto the subspace capital v of the vector x. 3d projections use the primary qualities of an object s basic shape to create a map of points that are then connected to one another to create a visual element. The vector projection of a vector a on or onto a nonzero vector b sometimes denoted proj b a displaystyle operatorname proj mathbf b mathbf a also known as the vector component or vector resolution of a in the direction of b is the orthogonal projection of a onto a straight line parallel to b. It is a vector parallel to b defined as.

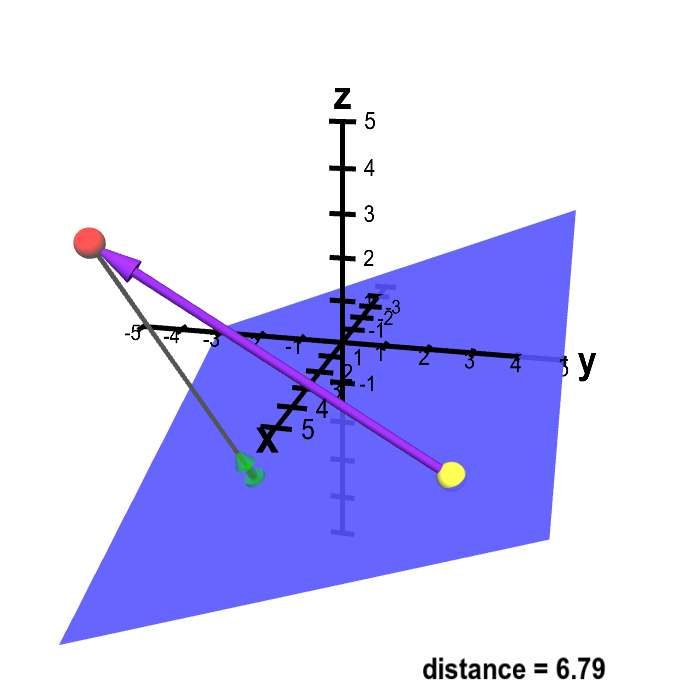
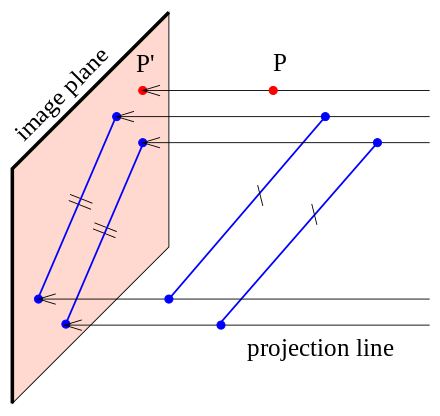
The result is a graphic that contains conceptual properties to interpret that the figure or. You could see if you take v plus w you re going to get x. The vector starts at the red circle and ends at the black circle representing the plane normal. The orientation of the plane is defined by its normal vector b as described here.

A b the component of line a that is projected onto plane b in other words a vector to the point on the plane where if you take a normal at that point it will intercept the end of vector a. Example projection onto a plane in r 3 example projection onto another plane in r 3 example projection onto a 3 space in r 4 in the context of the above recipe if we start with a basis of w then it turns out that the square matrix a t a is automatically invertible. A 3d projection is a design technique used to display a three dimensional object on a two dimensional surface. A 1 a 1 b displaystyle mathbf a 1 a 1 mathbf hat b where a 1 displaystyle a 1 is a scalar called the.

If you think of the plane as being horizontal this means computing u minus the vertical component of u leaving the horizontal component. Vector3 projectonplane uses the two vector3 values to generate the position of vector in the planenormal direction and return the location of the vector3 on the plane. And then this is vector that goes up like this out of the plane orthogonal to the plane is w. To do this we will use the following notation.